
Matura 2016 (maj). Zadanie 4. Demografia
W pliku demografia.txt znajdują się informacje o urodzeniach, zgonach i ruchu naturalnym ludności w Polsce w roku 2009, w podziale na województwa i powiaty. Pierwszy wiersz w pliku jest wierszem nagłówkowym.
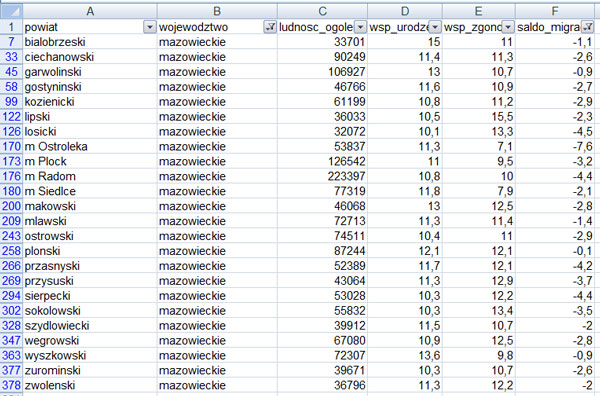
Fragment pliku demografia.txt:
| powiat | wojewodztwo | ludnosc_ogolem | wsp_urodzen | wsp_zgonow | saldo_migracji |
| augustowski | podlaskie | 58763 | 10,4 | 10,5 | -1,1 |
| bedzinski | slaskie | 150950 | 9,4 | 13 | 3,1 |
| belchatowski | lodzkie | 112993 | 11,5 | 9,1 | -1,6 |
Korzystając z dostępnych narzędzi informatycznych oraz danych zawartych w pliku demografia.txt, wykonaj podane polecenia. Odpowiedź do każdego zadania poprzedź numerem tego zadania.
Pobieranie danych do programu.
Zadanie 1.
Podaj liczbę powiatów należących do województwa mazowieckiego, w których saldo migracji było ujemne.
Rozwiązanie:
Komentarz:
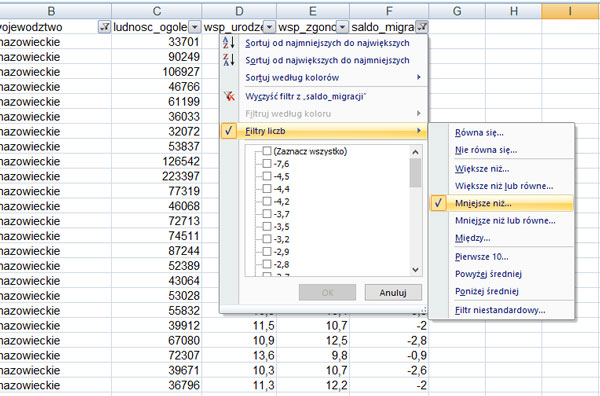
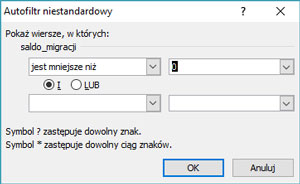
Do obliczenia ilości powiatów z województwa mazowieckiego, których saldo migracji jest ujemne należy użyć filtra dla województwa – ustalamy mazowieckie, zaś dla kolumny saldo_migracji używamy filtra liczb -> mniejsza niż -> ustalamy wartość na 0 (zero). Ilość wyświetlonych wierszy jest równa 24.
Zadanie 2.
Współczynnik przyrostu naturalnego to różnica pomiędzy współczynnikiem urodzeń a współczynnikiem zgonów. Utwórz zestawienie 10 powiatów o największym współczynniku przyrostu naturalnego zawierające nazwę powiatu i współczynnik przyrostu naturalnego. Zestawienie uporządkuj alfabetycznie.
Rozwiązanie:
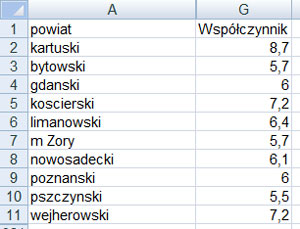
Komentarz:
Współczynnik przyrostu naturalnego obliczamy w nowej kolumnie G wykorzystując funkcję =D2-E2. Następnie sortujemy Z-A wg kolumny G. Następnie ukrywamy kolumny od B-F, a potem sortujemy wg powiatu tylko pierwszych dziesięć powiatów.
Zadanie 3.
Podaj nazwy czterech województw o największej liczbie ludności oraz liczbę ludności w tych województwach.
Rozwiązanie:
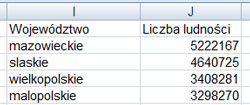
Komentarz:
W pierwszej kolejności należy wybrać wszystkie występujące województwa w naszym zestawieniu. Kolejnym krokiem jest obliczanie ilości mieszkańców dla każdego województwa, wykonujemy to za pomocą funkcji:
=SUMA.JEŻELI($B$2:$B$380;I2;$C$2:$C$380)
Zakres komórek z których sumujemy to wszystkie nazwy województw $B$2:$B$380, zaś suma to liczba mieszkańców w każdym powiecie należącym do województwa $C$2:$C$380. W funkcji tej występuję jeszcze I2, jest to nazwa województwa wpisana wcześniej. Sortujemy malejąco wg ilości sumy mieszkańców w danym województwie. Wybieramy pierwsze cztery rekordy.
Zadanie 4.
Współczynnik urodzeń to liczba urodzeń na 1000 mieszkańców, czyli:
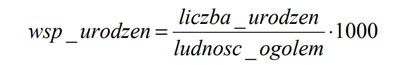
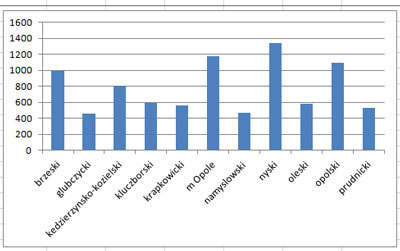
Na podstawie podanej liczby ludności każdego powiatu (ludność ogółem) oraz współczynnika urodzeń w tym powiecie wykonaj dla województwa opolskiego zestawienie powiatów oraz liczby urodzeń w 2009 roku w każdym powiecie. Obliczoną liczbę urodzeń zaokrąglij w dół do najbliższej liczby całkowitej. Zestawienie posortuj alfabetycznie. Na podstawie powyższego zestawienia utwórz wykres kolumnowy ilustrujący liczbę urodzonych dzieci w poszczególnych powiatach. Pamiętaj o prawidłowym opisie wykresu.
Rozwiązanie:
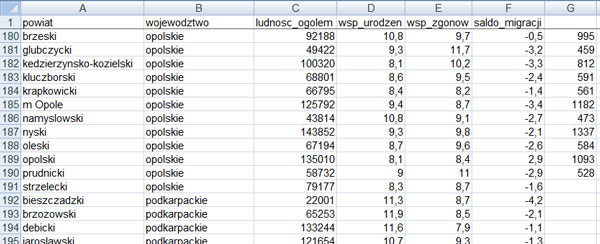
Komentarz:
Rozwiązywanie zadania należy rozpocząć od wykonania sortowania wg województw, ponieważ musimy wykonać tylko dla województwa opolskiego. Następnie dla nowej kolumny tworzymy formułę odwrotną obliczającą liczbę urodzeń ze wzoru:
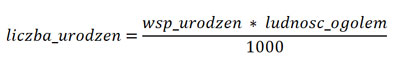
dzięki przekształceniu wzoru została utworzona formuła: =ZAOKR.DÓŁ(D180*C180/1000;0)
Na zakończenie tworzymy wykres z danych: nazwy powiatu województwa opolskiego i danych z kolumny G.

